Die Schülerin Regina Quelibari und Leonard Wölfl haben untersucht, welche Experimente mit dem Rotationssensor (Gyrometer) des Smartphones im Physikunterricht möglich sind:

 

1. 1. 1. Wissenschaftliches Poster zur Präsentation der Ergebnisse bei der Ausstellung

      2. Erklärung der Funktion des Sensors

      3. Experiment: Drehbewegungen im Alltag

      4. Experiment: Pirouetteneffekt

      5. Experiment: Winkelgeschwindigkeit und Radialbeschleunigung einer Haustüre

      6. Experiment: Radius eines Kreisverkehrs

      7. Geeignete Apps für Experimente mit den Rotationssensor

      8. Literatur zu den durchgeführten Experimenten und weitere Ideen

 

 

1. Wissenschaftliches Poster zur Präsentation der Ergebnisse bei der Ausstellung

Download Poster: DINA3 PDF	Experimente am Ausstellungsstand zum Rotationssensor.

 

 

zur Übersicht

 

 

 

2. Erklärung der Funktion des Sensors

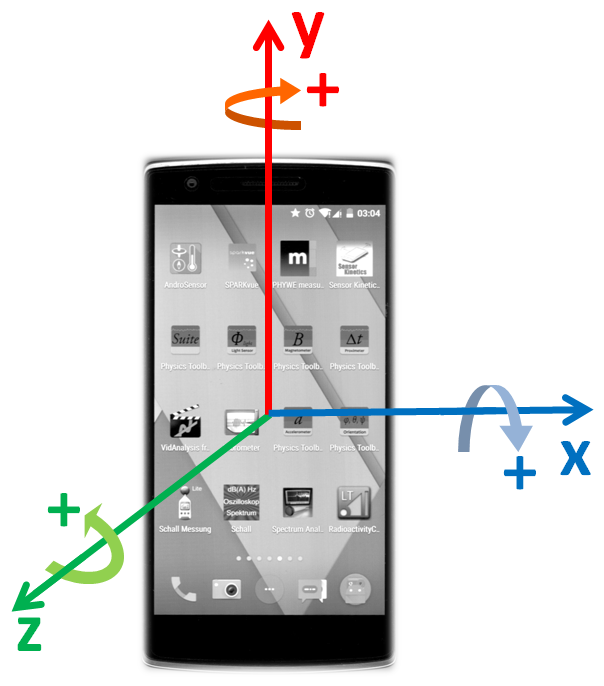	Ein Gyrometer ist ein Sensor zur Aufnahme der Drehgeschwindigkeit eines Körpers. Der Name leitet sich aus dem griechischen gyros = Drehung und skopein = sehen ab. Der Sensor ermittelt um welchen Winkel Δ φ sich ein Körper in der Zeit Δ t gedreht hat und bestimmt daraus die Drehgeschwindigkeit ω: ω = Δ φ / Δ t. Die Drehgeschwindigkeit wird auch als Winkelgeschwindigkeit bezeichnet und kann im Gradmaß [°/s] oder im Bogenmaß [rad/s] angegeben werden. Ein einzelner Rotationssensor kann Winkelgeschwindigkeiten nur entlang von einer Drehachse erfassen. Um Rotationen in jede Richtung zu messen, besitzt ein Smartphone drei dieser Sensoren, die rechtwinklig zueinander angeordnet sind (x-, y- und z-Achse). Die positive Drehrichtung lässt sich dabei wie bei magnetischen Feldlinien mit der rechten Faustregel ermitteln: Daumen = Richtung der Achse, Fingerspitzen = positive Drehrichtung. Die Rotation um die drei Raumachsen wird häufig auch als  gieren (yaw: Drehung um die Hochachse y), nicken (nick - Drehung um die Querachse x) und rollen (roll - Drehung um die Längsachse z) bezeichnet.
	Das Grundprinzip eines Gyrometers ist ein kardanisch aufgehängter Kreisel, der sich mit einer hohen Geschwindigkeit um seine Achse dreht. Wenn sich die Lage des äußeren Systems verändert behält der Kreisel aufgrund der Drehimpulserhaltung seine ursprüngliche Orientierung im Raum bei. Durch die Messung der Abweichung zwischen Drehachse des Kreisels und dem äußerem System lässt sich die Lage im Raum über drei Winkel in Bezug zur x-, y- und z-Achse vollständig bestimmen.  In Smartphones befinden sich keine drehenden Kreisel sondern sogenannte Vibrationskreisel. Vom Prinzip her besteht ein solcher Sensor aus einem Fadenpendel, das bei einer Änderung des äußeren Systems in der ursprünglichen Schwingungsebene pendeln möchte. Ein bekanntes Beispiel hierfür ist das Foucault-Pendel zur Bestimmung der Erdrotation.
	Statt eines Fadenpendels wird in einem Smartphones ein mikromechanischer schwingender bzw. vibrierender Stab eingesetzt. Der Stab ist in der Mitte fixiert - die beiden Enden schwingen in einer Ebene. Bei einer Drehung des äußeren Rahmens nach rechts oder links möchten die schnell schwingenden Enden des Stabes aufgrund der Massenträgheit in der Schwingungsebene bleiben und verzerren sich dadurch. Die Amplitude der Verzerrung wird über Piezzoelemente gemessen und in die Winkelgeschwindigkeit ω umgerechnet.
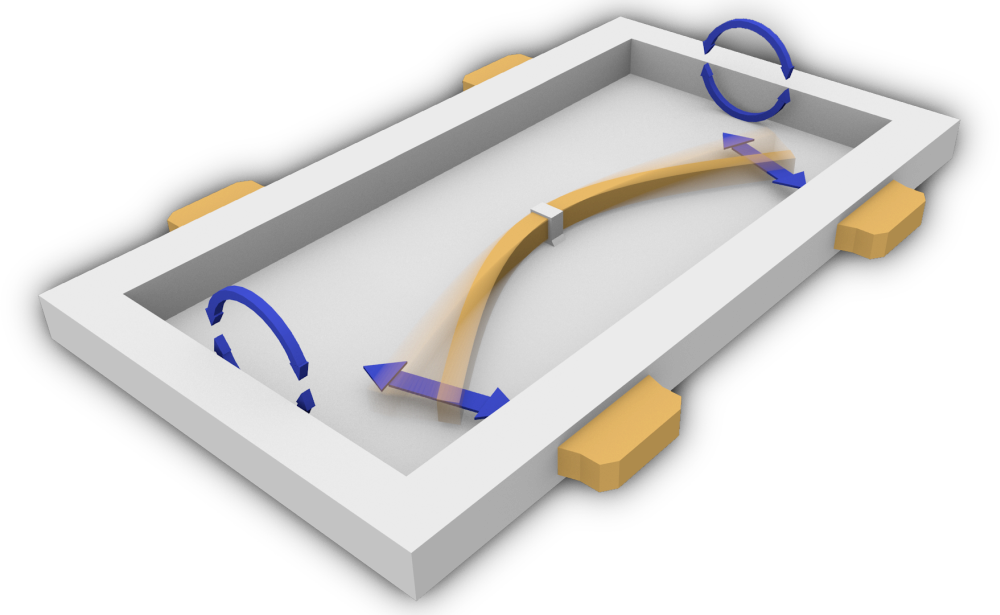	Abgeschaut wurde das Prinzip des Vibrationskreisels aus der Natur: Insekten wie z. B. Schnaken können sich mit dem schnellen Flügelschlag ihrer Schwingkölbchen und der möglichen Verzerrung perfekt im Raum orientieren. Eine schöne Animation ist im YouTube-Video: "How it works - The Vibrating Gyro" zu finden. Im Gegensatz zum drehenden Kreisel kann mit dem Vibrationskreisel nur die Winkelgeschwindigkeit ω und nicht die exakte Lage im Raum bestimmt werden. Zur Messung der räumlichen Bewegung eines Smartphones werden die Messdaten von Beschleunigungs- Rotations- und Magnetfeldsensoren miteinander verknüpft.

 

zur Übersicht

 

 

 

3. Experiment: Drehbewegungen im Alltag

Forschungsfrage: Welche Drehbewegungen im Alltag lassen sich mit dem Gyrometer messen?

Drehbewegungen gibt es überall: Am Fahrrad, bei der Waschmaschine, in der Küche, .... . Mit einer Salatschleuder konnte gezeigt werden, dass der maximale Messbereich des Gyrometers ω_max = ± 2295°/s ist. Dies entspricht U = 382rpm (rounds per minute - Umdrehungen pro Minute). Die Messung des zeitlichen Verlaufs der Schleuderbewegung einer Waschmaschine (U = 1.400rpm) wäre mit dem Smartphone somit nicht mehr möglich. Auch die im Smartphone eingebauten Beschleunigungssensoren erreichten in der Salatschleuder den maximalen Messbereich von a_max = ± 40m/s².

 

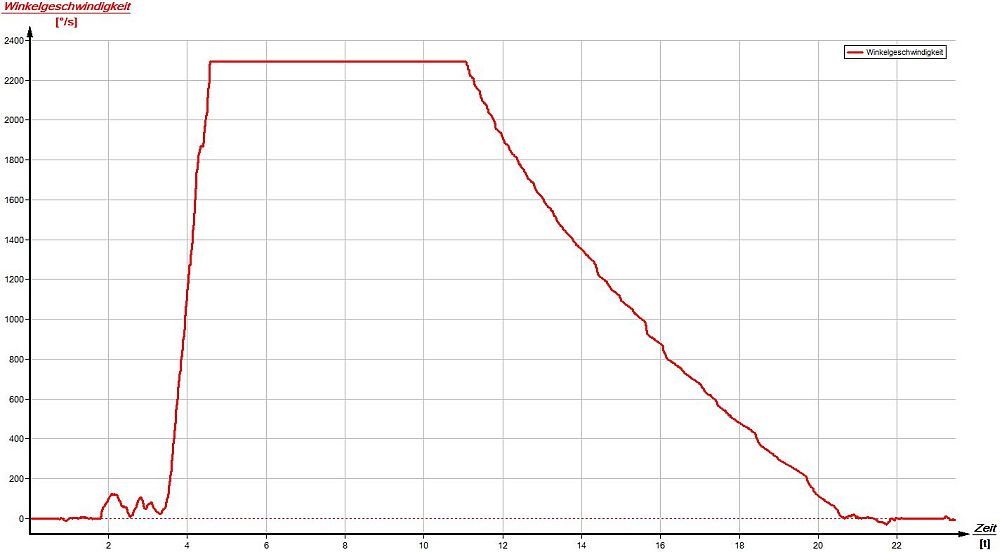Smartphone in der Salatschleuder.	Maximaler Messbereichs des Smartphones.

 

Weniger turbulent ging es dagegen auf dem Kinderspielplatz zu: Mit dem Smartphone wurde die Winkelgeschwindigkeit (Drehung um die z-Achse) eines Spielplatz-Kreisels bestimmt. So richtig viel Spaß machte es ab ω = 120°/s = 20rpm. Deutlich ist in der Messung die Dämpfung der Drehbewegung aufgrund der Reibung erkennbar.

 

Smartphone mit den Schülern auf dem Kinderspielplatz.	Erst eine Drehung nach links, dann nach rechts und wieder links.

 

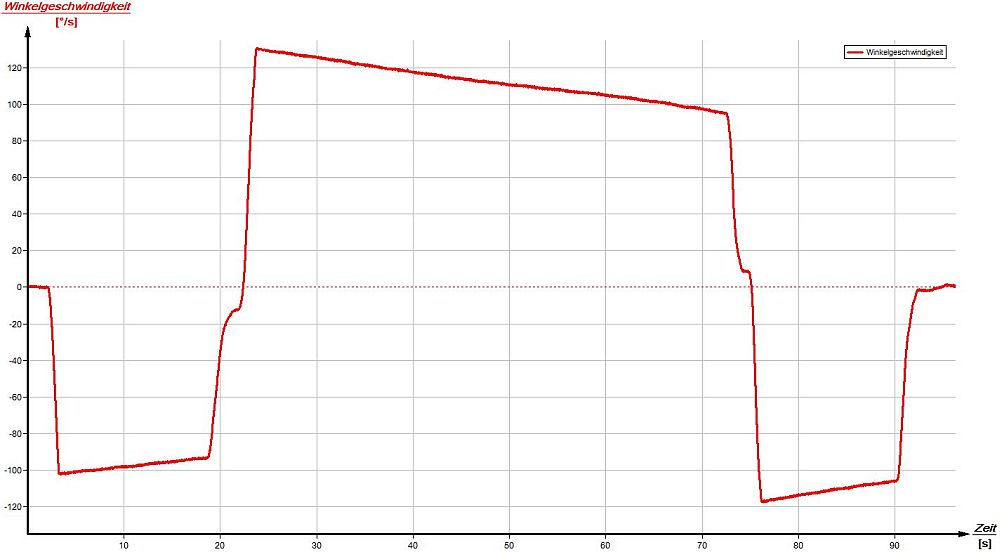
So richtig nostalgisch wurde es mit dem Plattenspieler "Dual P51" aus der Physiksammlung: Baujahr 1970! Das Gerät ist noch voll funktionsfähig und spielte Hits des Schlagerstars "Jürgen Marcus" aus dem Jahre 1976. Über das Smartphone wurden die Schlagersongs zunächst mit den Hits aus dem Jahre 2015 verglichen und im Anschluss die beiden Winkelgeschwindigkeiten des Plattenspielers bestimmt. Die kleinere Geschwindigkeit (U = 33,33rpm) dient zum Abspielen von großen Langspielplatten. Mit der größeren Geschwindigkeit  (U = 45rpm) konnte die Single-Platte von Jürgen Marcus zum Leben erweckt werden. Die Messung ergab bei der Einstellung "45" eine konstante Winkelgeschwindigkeit von ω = 284°/s = 47,3rpm. Bei der Einstellung "33" ergab sich eine Winkelgeschwindigkeit von ω = 210°/s = 35rpm. Die Abweichung zwischen Messung und Theorie ist evtl. über die ab 1987 schleichend angehobene Netzspannung von U = 220V auf U = 230V erklärbar.

 

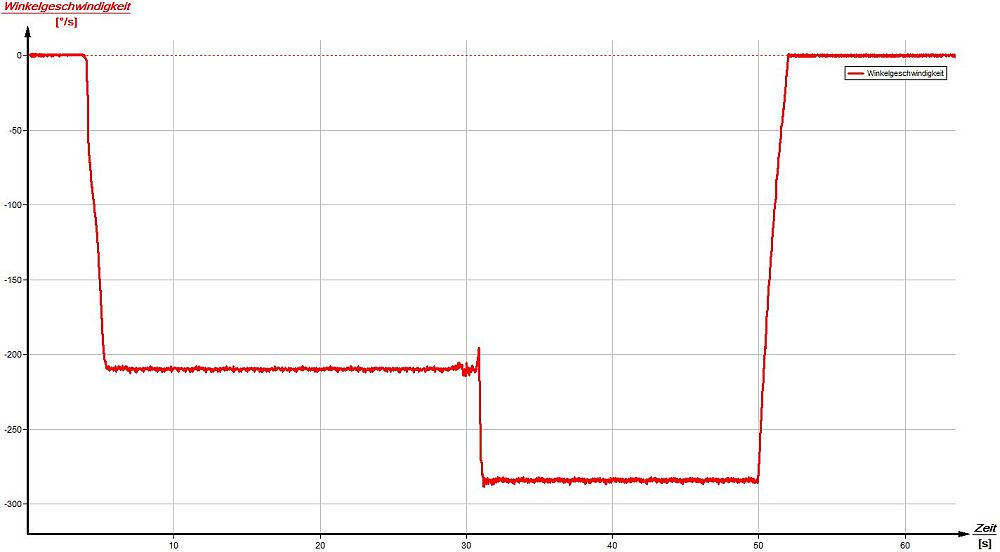Schallplattenspieler mit Smartphone und Musik von 1976.	Konstante Winkelgeschwindigkeiten in zwei Stufen.

 

Hohe Winkelgeschwindigkeiten kann man z. B. im Fahrgeschäft "Breakdance" auf dem Jahrmarkt erleben. Das rasante Fahrvergnügen kommt durch drei Kreisbewegungen zustande, die sich gegenseitig überlagern:

• Der äußere Kreis dreht sich mit allen 16 Gondeln.
• Jeweils vier Gondeln sind miteinander gruppiert und drehen sich um den gemeinsamen Mittelpunkt.
• Jede Gondel kann alleine um die eigene Achse rotieren.

Am Anfang sind die Kreisbewegungen noch langsam. Nach t = 90s Fahrt erreichen die Gondeln eine Winkelgeschwindigkeit von φ = 401°/s = 66rpm. Der Fahrspaß kommt nicht nur durch die hohe Winkelgeschwindigkeit zustande, sondern vor allem durch die schnelle Änderung von einer Links- in eine Rechtsdrehung: Innerhalb von Δt = 2s beträgt die maximale Änderungsrate Δφ_max = 709° (zur Zeit t = 91s).

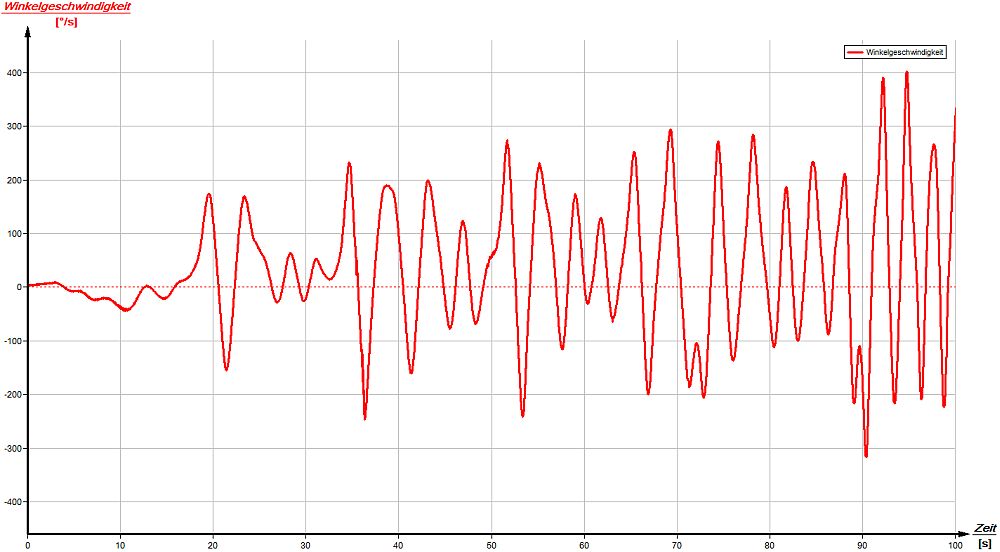"Breakdance" auf der Freiburger Frühjahresmesse.	Winkelgeschwindigkeiten während den ersten 100 Sekunden Fahrt.

 

zur Übersicht

 

 

 

4. Experiment: Pirouetteneffekt

Forschungsfrage: In welchem Verhältnis ändern sich die Winkelgeschwindigkeiten auf einem Drehstuhl?

Beim Pirouetteneffekt nimmt die Drehgeschwindigkeit eines Körpers zu, sobald sich die Massen näher an seine Rotationsachse verlagern. Der Effekt wird in vielen Sportarten wie dem Eiskunstlauf, dem Ballett, dem Rollkunstlauf oder dem Turmspringen bei Drehungen um die eigene Körperachse eingesetzt. Die physikalische Grundlage für den Pirouetteneffekt ist die Drehimpulserhaltung: L = konstant. Der Betrag des Drehimpulses L berechnet sich als Produkt von Trägheitsmoment θ und Winkelgeschwindigkeit ω: L = θ · ω. Je größer das Trägheitsmoment θ eines rotierenden Körpers wird, desto kleiner muss die Winkelgeschwindigkeit ω werden, da der Drehimpuls L des Körpers konstant bleibt.

Das Trägheitsmoment θ hängt von der Verteilung der Masse in Bezug auf die Rotationsachse ab. Je weiter die Massen vom Drehzentrum entfernt sind, desto größer wird das Trägheitsmoment. Dreht sich eine punktförmige Masse m mit dem Radius r um einen Mittelpunkt berechnet sich das Trägheitsmoment als Produkt von Masse m und dem Quadrat des Radius r:  Θ = m · r².

 

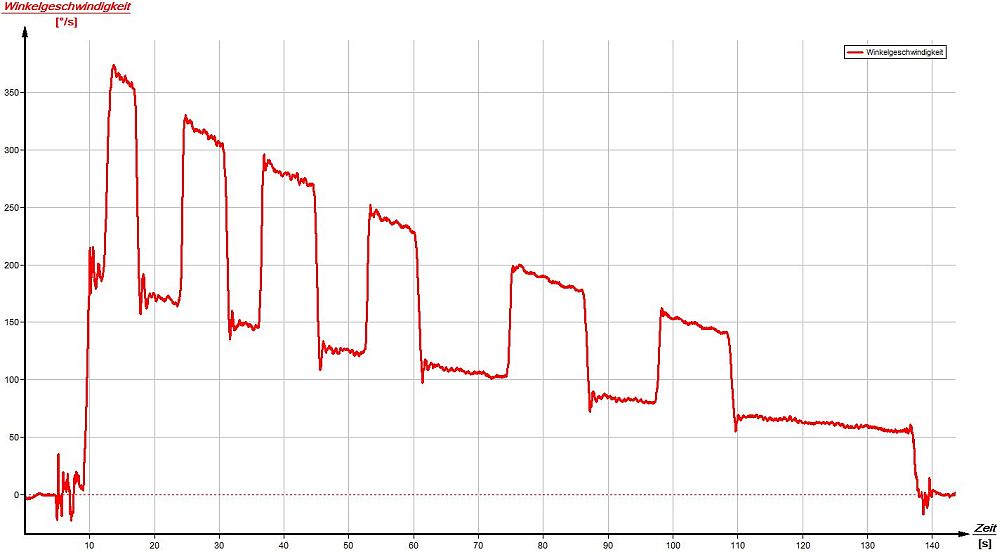
Drehstuhl mit Smartphone zur Messung von ω. Zwei Kugelgewichte der Masse von je m = 1,5kg.	Änderung der Winkelgeschwindigkeit: Sechsmaliges Ausstrecken der Arme mit den Gewichten.

 

Für das Experiment saß ein m = 70kg schwerer Schüler auf einem Drehstuhl und hatte jeweils ein Gewicht der Masse m = 1,5kg in beiden Händen. Zur Messung wurde das Smartphone mit doppelseitigem Klebeband auf den Boden des Drehstuhls geklebt. Während des Experimentes zog der Schüler die Arme insgesamt sechsmal nach innen. Die Winkelgeschwindigkeit ω wurde dabei mit der kostenlosen App "Physics Toolbox" aufgenommen.

Die maximale Winkelgeschwindigkeit bei angezogenen Armen betrug ω = 374°/s = 62rpm. Deutlich ist in der Messkurve die Dämpfung der Kreisbewegung aufgrund des Luftwiderstandes und der Reibung des Drehstuhls erkennbar. Nach der Zeit von  t = 130s hatte der Schüler insgesamt φ = 19.711° an Drehung hinter sich (Bestimmung von  φ über das Integral der Messkurve), was insgesamt 55 Umdrehungen entspricht. Eine intensive Nachbetreuung des Schülers war umgehend notwendig.

Aufgrund der Drehimpulserhaltung bei ausgestreckten bzw. angezogenen Armen: L_ausgestreckt = L_angezogen = konstant und des des immer gleichen Verhältnisses der Trägheitsmomente: Θ_ausgestreckt / Θ_angezogen = konstant muss das Verhältnis der Winkelgeschwindigkeiten ω_schnell / ω_langsam ebenso konstant sein. Dies wurde durch die sechsfache Messung der Unterschiede der Winkelgeschwindigkeiten experimentell bestätigt: ω_schnell / ω_langsam = 2,2 ± 0,1.

zur Übersicht

 

 

 

5. Experiment: Winkelgeschwindigkeit und Radialbeschleunigung einer Haustüre

Forschungsfrage: Lässt sich aus den Messdaten einer Kreisbewegung der Drehradius bestimmen?

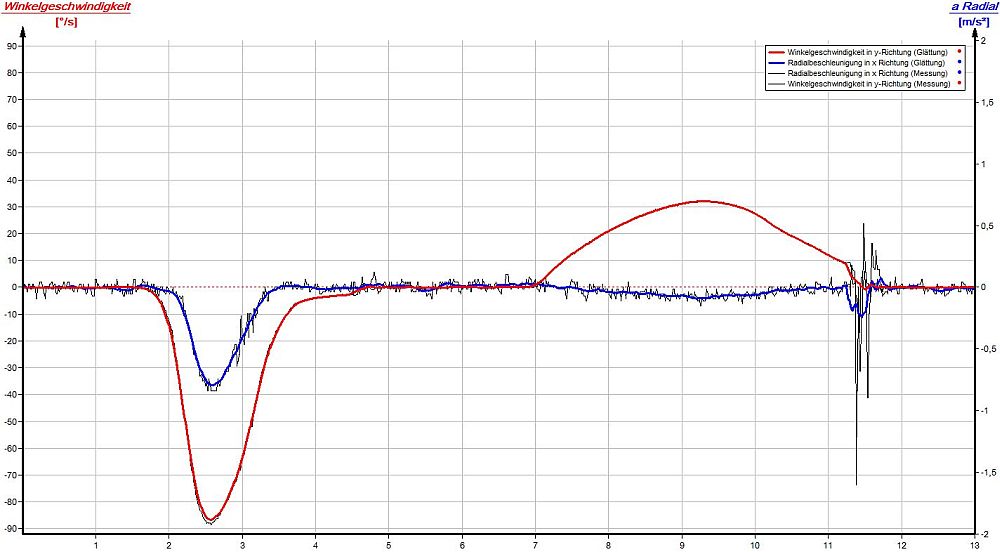
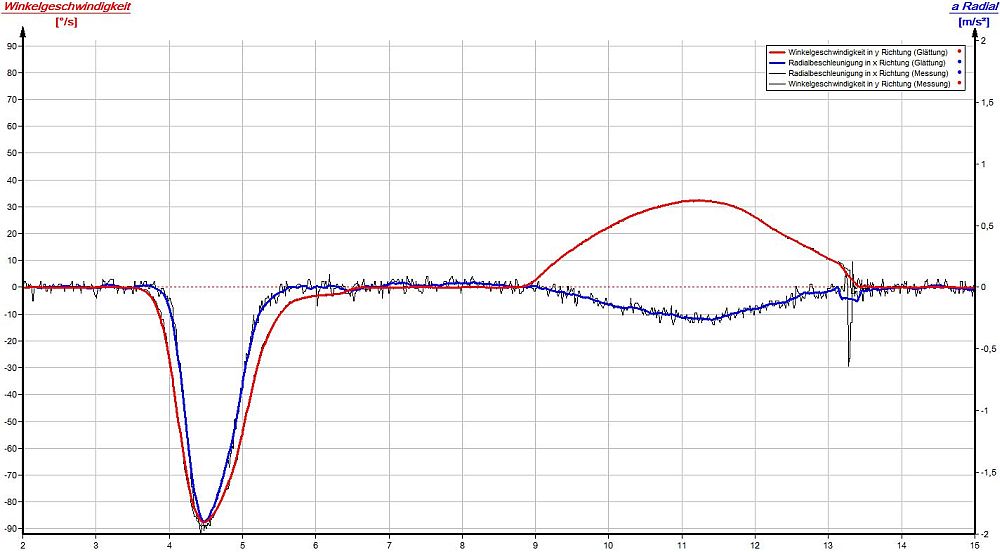
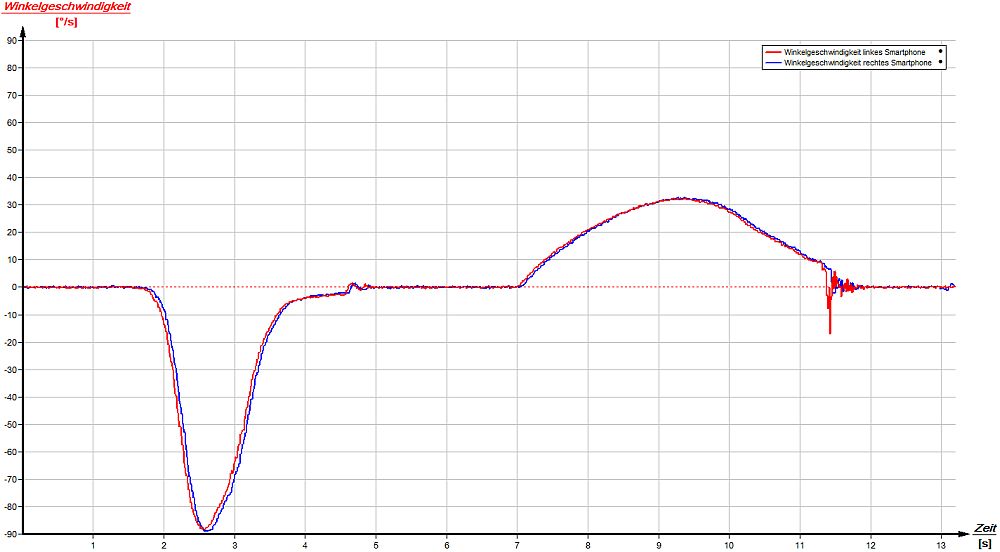
Die Winkelgeschwindigkeit ω ist unabhängig vom Radius eines Körpers zu seiner Drehachse. Zum Beweis der Behauptung wurden zwei Smartphones zur Messung der Winkelgeschwindigkeit an zwei Orten eines Querholms einer Haustüre angebracht [1], [2]. Aus der Messkurve geht hervor, dass zur Zeit t = 2s die Türe mit einem Schwung geöffnet wurde. Zur Zeit t = 4,6s schlägt die Tür links am Türstopper an. Danach blieb die Türe für t = 2s lang geöffnet und ist über den mechanischen Türschließer wieder ins Schloss gefallen. Deutlich ist danach (t = 11,4s) das Schwingen des Querholms der Türe erkennbar. Die Messung der Drehbewegung erfolgte mit der kostenlosen App "AndroSensor" und wurde nacheinander gestartet. Im Diagramm (rot = linkes Smartphone, blau = rechtes Smartphone) zeigt sich eine vom Radius unabhängige Winkelgeschwindigkeit.

Zwei Smartphones an einer Haustüre mit unterschiedlichem Radius zur linken Drehachse der Tür.	Messung der Winkelgeschwindigkeit: rot: linkes Smartphone - blau: rechtes Smartphone

 

Über das Integral der "Öffnungskurve" (t = 1 - 6s) ergab sich im kostenlosen Programm "Phywe Measure" ein Winkel der Türöffnung von φ = 91°. Das Integral der "Schließungskurve" (t = 6 - 13s) ergab einen Winkel von φ = 92°. Beide Messwerte entsprechen der Realität: Die Türe kann um φ = 90° geöffnet werden.

Bei einer Kreisbewegung lässt sich die Geschwindigkeit v eines Objekts als Vektor mit einer bestimmten Richtung und Länge darstellen. Der Betrag der Geschwindigkeit v ist bei einer gleichmäßigen Rotation konstant, die Richtung des Vektors ändert sich jedoch immer. Bei einer kontinuierlichen Kreisbewegung muss somit eine Beschleunigung a wirken, die als Vektor zum Kreismittelpunkt zeigt. Der Betrag der sogenannten Radial- oder Zentripetalbeschleunigung a_R berechnet sich als Produkt aus Radius r und dem Quadrat der Winkelgeschwindigkeit ω:  a_R = r · ω². Eine Animation zur Herleitung der Zusammenhänge ist auf der Homepage von Leifi-Physik verfügbar.

 

Gleichzeitige Messung am linken Smartphone: rot = Winkelgeschwindigkeit, blau = Radialbeschleunigung.	Gleichzeitige Messung am rechten Smartphone: rot = Winkelgeschwindigkeit, blau = Radialbeschleunigung.

 

Bei der Türbewegung wurde die Radialbeschleunigung a_R mit dem internen Beschleunigungssensor des Smartphones in x-Richtung und die Winkelgeschwindigkeit ω mit dem internen Rotationssensor in y-Richtung gleichzeitig aufgenommen. In den beiden Diagrammen ist deutlich die Abhängigkeit der Radialbeschleunigung a_R vom Radius r zu erkennen. Zur Bestimmung von r wurde in einem weiteren Diagramm auf der x-Achse ω [rad/s] und auf der y-Achse a_R  [m/s²] aufgetragen. Über die Funktionsanpassung mit einer Normalparabel f (x) = r · x² (a_R = r· ω²) kann aus den Messwerten der Faktor r [m] bestimmt werden: r_links = 31,9cm, r_rechts = 80,7cm. Zum Vergleich der Werte für r wurde der Abstand zusätzlich mit einem Maßband gemessen: r_links = 36cm, r_rechts = 84cm. Gründe für die Abweichung können die große Streuung der Beschleunigungswerte für a_R < 0,2m/s² oder die nicht mittige Anbringung des Beschleunigungssensors im Smartphone sein.

 

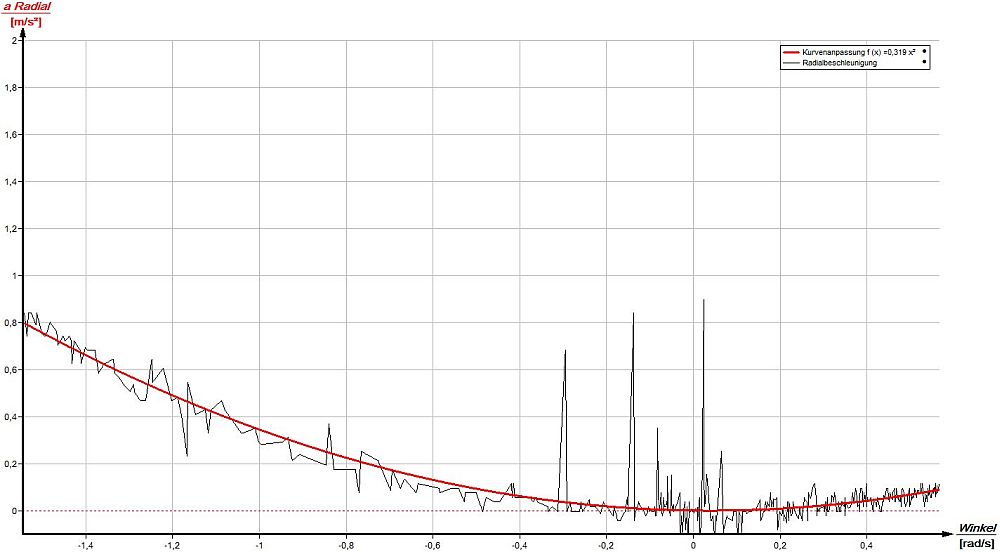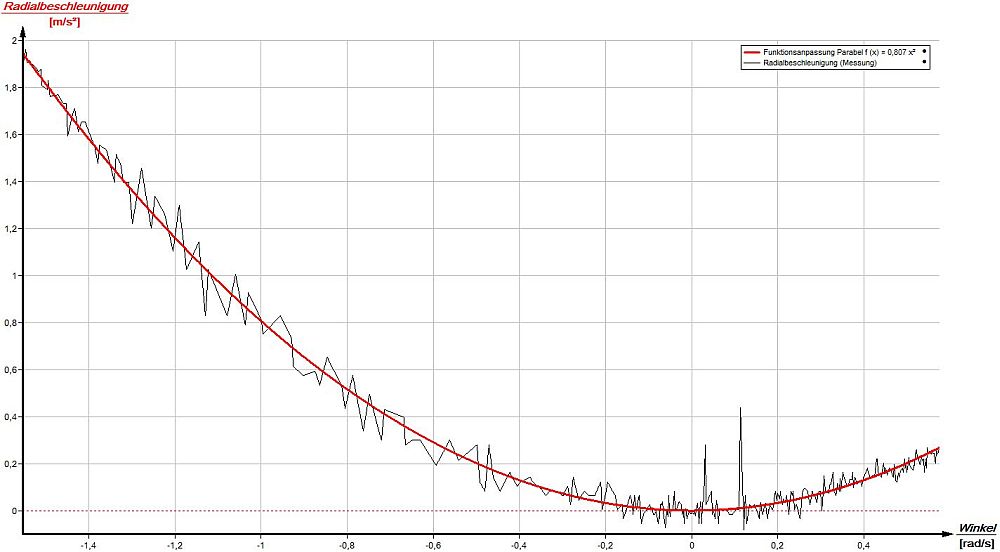Bestimmung des Radius r des linken Smartphones über eine Funktionsanpassung: r = 31,9cm.	Bestimmung des Radius r des rechten Smartphones über eine Funktionsanpassung: r = 80,7cm.

 

zur Übersicht

 

 

 

6. Experiment: Radius eines Kreisverkehrs

Forschungsfrage: Kann mit dem Gyrometer der Radius eines Kreisverkehrs bestimmt werden?

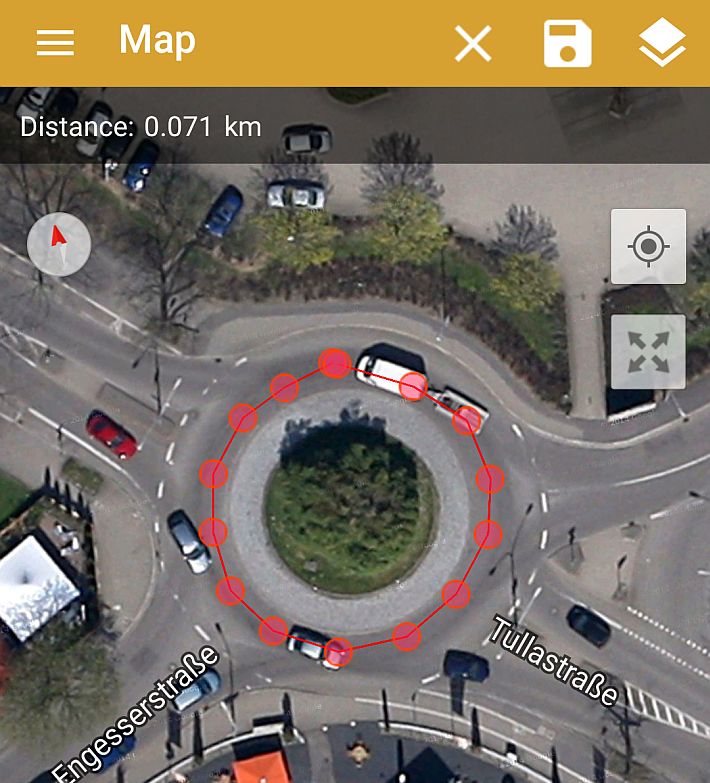
Wie im vorherigen Türexperiment gezeigt lässt sich mit Hilfe des Rotations- und Beschleunigungssensors die Breite einer Türe bestimmen. Das gleiche Experiment wird nun in größeren Dimensionen wiederholt: Mit einem Auto wurde ein Kreisverkehr in der Nähe der Schule mehrmals durchfahren [2], [3]. Das Smartphone war dabei mit doppelseitigem Klebeband auf dem Armaturenbrett des Autos befestigt. Die Messung der Rotation um die z-Achse und der Beschleunigung in x-Richtung erfolgte mit der kostenlosen App "AndroSensor".  Beim Start der Messkurve befand sich das Auto bereits im Kreisverkehr. Nach ca. drei Runden fuhr das Auto zur Zeit t = 33s mit einer Rechtskurve aus dem Kreisverkehr heraus und danach geradeaus weiter.

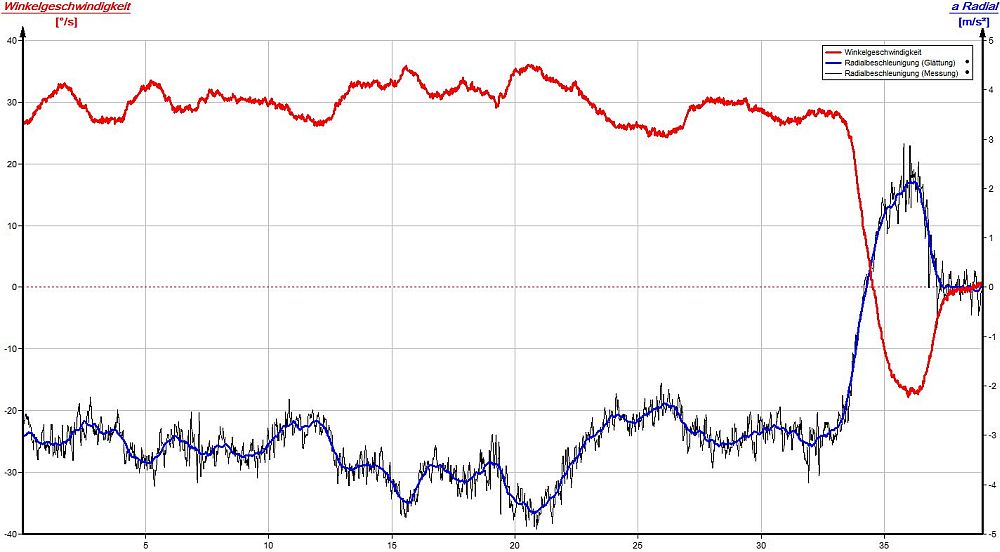Kreisverkehr in Freiburg an der Kreuzung Tullastraße / Engesserstraße.	Messergebnis Smartphone: rot: Winkelgeschwindigkeit, blau: Radialbeschleunigung.

 

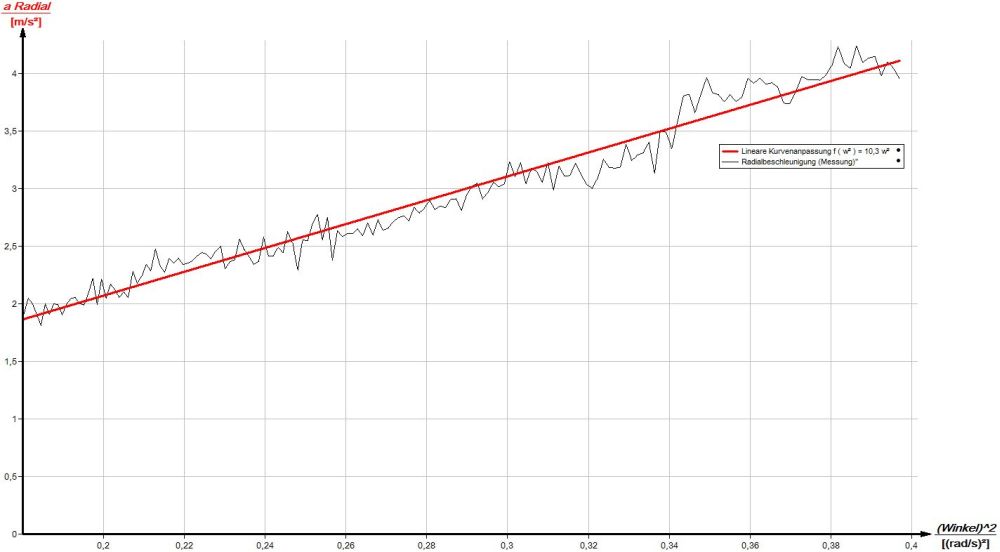
Zur Bestimmung von r über die Formel a_R = r· ω² wurde in einem weiteren Diagramm auf der x-Achse ω² [(rad/s)²] und auf der y-Achse a_R [m/s²] aufgetragen. Über die Funktionsanpassung mit einer linearen Funktion f(x) = r · x kann aus den Messwerten der Faktor r [m] bestimmt werden: r = 10,3m. Ein Vergleich des berechneten Wertes von r mit einer Maßbandmessung war aufgrund der Sträucher in der Mitte des Kreisverkehrs und des hohen Verkehrsaufkommens nicht möglich. Der Radius wurde deshalb über zwei andere Verfahren ermittelt: Zunächst wurde mit der kostenlosen App "GPS Fields Area Measurement" (siehe Gruppe 5: Experiment 7)  der Umfang des Kreisverkehrs ermittelt und daraus der Radius berechnet: r = 11,3m. Danach erfolgte die Bestimmung von r über die Längenmessung bei Google-Maps: r = 10,9m. Alle drei Messungen liefern ähnliche Ergebnisse mit einer maximalen Abweichung von Δr = 1m.

 

Messung mit einer GPS App: U = 71m,  r = 11,3m.	Funktionsanpassung mit linearer Funktion zur Bestimmung des Radius r aus den Messdaten: r = 10,3m.	Messung mit der Längenmessung von Google-Maps: r = 10,9m.

 

 

zur Übersicht

7. Geeignete Apps für Experimente mit dem Rotationssensor

Für die Experimente auf dieser Homepage wurden die folgenden kostenlosen Apps eingesetzt:

System	Name der App	Vor- und Nachteile der App	Symbol	QR Code
Android	AndroSensor	Vorteile: Alle interne Sensoren messbar, Export der Daten aller Sensoren Nachteil: Export: Formatierung Dezimaltrennzeichen
Android	Physics Toolbox Suite	Vorteile: Alle internen Sensoren messbar, viele Einstellmöglichkeiten, Export von Daten Nachteil: Export von Daten nur von einem Sensor.
iOS	SensorLog	Vorteile: Alle internen Sensoren messbar, viele Einstellmöglichkeiten. Nachteil: Export von Daten nur über iOS Server.

 

zur Übersicht

 

8. Literatur zu den durchgeführten Experimenten und weitere Ideen

 

• • [1] P. Klein, J. Kuhn, A. Müller: Zerschlagen einer Tür als Anwendungsbeispiel der Rotationsdynamik, in: Unterricht Physik (2015), H. 145, S. 21–23.

  • [2] M. Monteiro et al.: Angular Velocity and Centripetal Acceleration Relationship, in: The Physics Teacher, 52. Jg. (2014), H. 5, S. 312–313.

  • [3] L. Resta, Z. Trzmiel: Beschleunigungsmessung mit dem Smartphone, iStage 2.

  • [4] A. Shakur, T. Sinatra: Angular momentum, in: The Physics Teacher, 51. Jg. (2013), H. 9, S. 564–565.

  • [5] F. Tornaría, M. Monteiro, A. C. Marti: Understanding coffee spills using a smartphone, in: The Physics Teacher, 52. Jg. (2014), H. 8, S. 502–503.

 

zur Übersicht

zur Startseite

 

 

Autoren / Bilder / Experimente:
Regina Quelibari und Leonard Wölfl, Schüler der Kursstufe II, Abitur 2015, Friedrich-Gymnasium Freiburg
Dr. Patrick Bronner, Physiklehrer, Friedrich-Gymnasium Freiburg

CC BY-NC-SA 4.0 © Patrick Bronner (Friedrich-Gymnasium Freiburg / mascil project)