Auf dieser Seite geht es um die Mischung von Champagnertrüffel.

Aufgabe: Marzipan-Mischung
Sie bieten Champagnertrüffel zum Preis von 3,70 €/100 g sowie Walnuss-Marzipan für 3,40 €/100 g an.
a) Sie wollen die Pralinen zu gleichen Teilen gemischt anbieten. Welchen Preis können Sie für 100 g verlangen?
b) Sie wollen eine Mischung erstellen, in der Sie doppelt so viele Champagnertrüffel wie Walnuss-Marzipan verwenden. Wie viel kosten jetzt 100 g?
c) In welchem Verhältnis müssen Sie die Pralinen mischen, damit sich ein Mischungspreis von 3,50 € ergibt?

CC by nc sa josef_tuerk

Mögliche Lösung:
3,40 €+3,70 €=7,10 €  kosten 200 g
7,10 €∶2= 3,55 €  kosten 100 g
2 ∙ 3,70 € + 3,40 €= 10,80 €  kosten 300 g
10,80 €∶3 = 3,60 €  kosten 100 g
Mischungsverhältnis 1 zu 2, d. h.   1/3 Champagnertrüffel,   2/3 Walnuss-Marzipan

Didaktisch-methodische Hinweise:
Insbesondere bei Aufgabenteil c) sind ganz unterschiedliche Lösungsansätze und Lösungswege denkbar, zum Beispiel:

• Probierlösung: verschiedene Mischungsverhältnisse durchprobieren, Lösung durch inhaltlich-anschauliche Überlegungen der Art: Der neue Preis liegt näher am Preis für Walnuss-Marzipan. Der Unterschied des Mischungspreises zum Preis von Walnuss-Marzipan (10 ct) ist halb so groß wie der zum Preis der Champagnertrüffel (20 ct). Deshalb nimmt man doppelt so viel Walnuss-Marzipan wie Champagnertrüffel.
• Lösung durch eine Gleichung:
  x = Anteil der Champagnertrüffel, damit ist
  (1 – x) = Anteil des Walnuss-Marzipans.
  Die Gleichung  x ∙3,70 + (1 – x) ∙ 3,40 = 3,50
  hat die Lösung  x =  1/3  und damit  (1 – x) =  2/3
• Lösung mithilfe des Mischungskreuzes (durch inhaltliche Überlegungen zu stützen!)

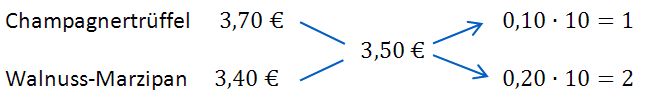
Die SchülerInnen sollten eigene Lösungswege finden, sich gegenseitig vorstellen, begründen und miteinander diskutieren können. 

Autoren: Thomas Reiner, Meinhard Petsch;